Orifices
ORIFICE
Classifications of orifices
1.The orifices are classified as small orifices and large orifices depending upon the size of orifice and head of liquid from the center of orifice. If the head of liquid from the center of orifice is more five times the depths of orifice, the orifice is called small orifice .And if the head of liquid is less than five times the depth of orifice, it is called large orifice.
2.The orifice are classified as
(1)circular orifice
(2)Triangular orifice
(3)Rectangular orifice
(4)Square orifice depending upon their cross-section areas
3.The orifices are classified as
(1)Sharp-edge orifice and
(2)Bell-mounted orifice depending upon the shape of upstream edge of orifice.
4.The orifices are classified as
(1)Free discharging orifice and
(2)Drowned and submerged orifice depending upon the nature of discharge.
The Sub-merged orifice are further classified as
(a)Fully-submerged orifice and
(b)Partially submerged orifice.
FLOW THROUGH AN ORIFICE
Consider a tank fitted with a circular orifice in one of its side as shown Let H be the head of the liquid above the center of orifice .The liquid flowing through orifice forms the jet of liquid whose area of cross section is less than that of orifice. The area of jet of fluid is goes on decreasing and at a section C-C the is minimum .This section is approximately at a distance of half of diameter of the orifice. At this section, the streamlines are straight and parallel to each other and perpendicular to the plane of the orifice. The section is called Vena-contracta. Beyond the section their jet diverges and is attracted in the downward direction by gravity
This is theoretical velocity.Actual velocity will be less than this value.
HYDRAULIC CO-EFFICIENTS
(1)Co-efficient of velocity(Cv), It is defined as the ratio between the actual velocity of jeyt of liquid at vena-contracta and the therotical velocity of jet .It is defined by Cv and mathematically Cv is given as
The value of Cv varies from 0.95 to 0.99 for different orifice ,depending upon the shape, size of the orifice and on the head under which flow take place .Genrally the value Cv=0.98 is used foe shaped edge orifice.
(2) Co-efficient of contraction (Cc), It is defined as the ratio of the area of the jet jet at vena contracta to the area of the orifice.It is defined as Cc.
a=area of orifice and
ac=area of jet at vena contracta
The value of Cc varies from 0.61 to 0.69 depending on the shape and size of the orifice and head of the liquid under which flow takes place .In general the vale of Cc may be takes as 0.64.
(3) Co-efficient of Discharge (Cd), It is defined as the ratio of actual discharge from an orifice to the theoretical discharge from the orifice .It is defined as Cd.
The value of Cd varies from 0.61 to 0.65 For genral purpose the value of Cd is taken as 0.62.
Example No.1. The head of water over orifice of diameter 40 mm is 10m.Find the actual discharge and actual velocity of jet at vena contracta .Take Cd=0.6 and Cv=0.98.
H=10cm,head
Diameter of orifice d=40mm=0.04m
Area (a)=0.785(0.04)2=0.001256m2
Cd=0.6 Cv=0.98
(1)
=0.6
(2)
(Example No.2). The head of water over the center of the orifice of diameter 20 mm is 1m .The actual discharge through the orifice is 0.85litre/s .find thee co-efficient of discharge.
D=20mm=0.02m
a=3.14/4(0.02)2=0.000314m2
H=1m
Q=0.85litre/s=0.00085m3/s
Flow or discharge through a large rectangular orifice
Let us consider a tank filled with liquid and also fixed with a large rectangular orifice. Let us think that rectangular orifice is fixed at one side of tank as displayed here in following figure.
Let us consider the following data from above figure.
H1 = Height of liquid surface from the top edge of the rectangular orifice
H2 = Height of liquid surface from the bottom edge of the rectangular orifice
Depth of rectangular orifice = H2- H1
b = Breadth of the rectangular orifice
d = Depth of rectangular orifice
d = H2- H1
Cd = Coefficient of discharge
Let us consider one elementary horizontal strip of depth dh at a depth of h, below the free surface of the liquid in the tank, in rectangular orifice as displayed in above figure.
Discharge through elementary horizontal strip,
In order to secure the expression for the flow or discharge through the entire rectangular orifice, we will integrate the above equation between the limits H1 and H2.
This is the expression for the flow or discharge through the large rectangular orifice.
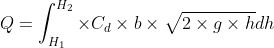
Example.1. Find the discharge through a rectangular orifice 2.0m wide and 1.5m deep fitted to a water tank in 3.0 m above the top edge of the edge of the orifice. Take Cd=0.62
Solution.
Width of orifice b=2.0m
Depth of orifice d=1.5m
Height of water above the top edge of the orifice,H1=3m
Height of water above the bottom edge of the orifice
H2=H1+d=3+1.5=4.5m
Cd=0.62
Discharge Q is given by equation
3.66[9.545-5.196]m3/s
=15.917m3/s
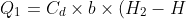\times&space;\sqrt{2gH})
![Q_{2}=\frac{2}{3}\times b\times \sqrt{2g}[H_{2}^{\frac{3}{2}}-H^{\frac{3}{2}}]](https://latex.codecogs.com/gif.latex?Q_{2}=\frac{2}{3}\times&space;b\times&space;\sqrt{2g}[H_{2}^{\frac{3}{2}}-H^{\frac{3}{2}}])
![=C_{d}\times b\times (H_{2}-H)\times \sqrt{2gH}+\frac{2}{3}\times b\times \sqrt{2g}[H_{2}^{\frac{3}{2}}-H^{\frac{3}{2}}]](https://latex.codecogs.com/gif.latex?=C_{d}\times&space;b\times&space;(H_{2}-H)\times&space;\sqrt{2gH}+\frac{2}{3}\times&space;b\times&space;\sqrt{2g}[H_{2}^{\frac{3}{2}}-H^{\frac{3}{2}}]) .................(7.10)
.................(7.10)
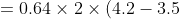\times&space;\sqrt{2\times&space;9.81\times&space;3.5})
=
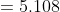
DISCHARGE THROUGH PARTIALLY SUB-MERGED ORIFICE
A partially submerged orifice is one which has its outlet side partially submerged under liquid as shown in Fig. 7.9. It is also known as a partially drowned orifice. Thus the partially submerged orifice has two portions. The upper portion behaves as an orifice discharging free while the lower portion behaves as a submerged orifice. Only a large orifice can behave as a partially submerged orifice. The total discharge Q through the partially submerged orifice is equal to the discharges through free and the submerged portions.
Fig. 7.9 Partially submerged orifice
Discharge through the sub-merged portion is given by equation (7.9)
Discharge through the free portion is given by equation (7.8) as
Thus,
Total Discharge Q = Q1+ Q2
Understand through youtube video: Click here
--------------------------------------------------------------------------------------------------------------------------
Problems:
1. A rectangular orifice of 2 m width and 1.2 m deep is fitted in one side of a large tank. The water level on one side of the orifice is 3 m above the top edge of the orifice, while on the other side of the orifice, the water level is 0.5 m below its top edge. Calculate the discharge through the orifice if Cd = 0.64.
Solution:
Given:
Width of orifice, b = 2 m
Depth of orifice, d = 1.2 m
Height of water from top edge of orifice, H1 = 3 m
Difference of water level on both sides, H = 3 + 0.5 = 3.5 m
Height of water from the bottom edge of orifice, H2 = HI + d = 3 + 1.2 = 4.2 m
The orifice is partially submerged. The discharge through the submerged portion,
=
The discharge through free portion is
Total discharge through the orifice is
========================================================================
References: 1. Fluid Mechanics by R. K. Bansal
DISCHARGE THROUGH FULLY SUB-MERGED ORIFICE
A fully submerged orifice is one which has its whole of the outlet side submerged under liquid so that it discharges a jet of liquid into the liquid of the same kind. It is also called totally drowned orifice. Fig. 7.8 shows the fully submerged orifice. Consider two points (1) and (2), point 1 being in the reservoir on the upstream side of the orifice and point 2 is at the vena-contracta as shown in Fig. 7.8.
Fig. 7.8 Fully submerged orifice
Let HI= Height of water above the top of the orifice on the upstream side,
H2 = Height of water above the bottom of the orifice,
H = Difference in water level,
b = Width of orifice,
Cd = Co-efficient of discharge.
Height of water above the center of the orifice on the upstream side
Height of water above the center of the orifice on the downstream side
Applying Bernoulli's equation at (1) and (2), we get
Now,
Understand with the help of youtube video: Click here
--------------------------------------------------------------------------------------------------------------------------
--------------------------------------------------------------------------------------------------------------------------
*PROBLEMS*
1. Find the discharge through a fully submerged orifice of width 2 m if the difference of water levels on both sides of the orifice be 50 cm. The height of water from the top and bottom of the orifice are 2.5 m and 2.75 m respectively. Take Cd = 0.6
Solution:
Given:
Width of orifice, b=2
Difference of water level, H= 50cm = 0.5 m
Height of water from top of orifice, H1= 50 cm =0.5 m
Height of watr from bottom of orifice, H2= 2.5m
Cd= 0.6
Discharge through fully submerged orifice is given by equation (7.9)
Or,
2. Find the discharge through a totally drowned orifice 2.0 m wide and I m deep, if the difference of water levels on both the sides of the orifice be 3 m. Take Cd = 0.62.
Solution:
Given:
Width of orifice, b=2 m
Depth of orifice, d=1 m
Difference of water level on both the sides
H = 3 m
Cd= 0.62
========================================================================
References:
1. Fluid mechanics by R. K. Bansal
========================================================================
1. Fluid mechanics by R. K. Bansal
========================================================================
TIME OF EMPTYING A TANK THROUGH AN ORIFICE AT ITS BOTTOM
Derivation:
Consider a tank containing a liquid upto a height of H1. Let an orifice is fitted at the bottom of the tank. It is required to find the time for the liquid surface to fall from the height H1 to height H2 .
Let, A = Area of the tank
a = Area of the orifice
H1 = Initial height of the liquid
H2 = Final height of the liquid
T = Time in seconds for the liquid to fall from H1 to H2 .
Let at any time, the height of liquid from orifice is h and let the liquid surface fall by a small height dh in time dT.
Then,
Volume of liquid leaving the tank in time,dT = A × dh
Also,
The theoretical velocity through orifice,
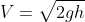
Discharge through orifice/sec
dQ = Cd × Area of orifice × Theoretical velocity
= Cd.a.√2gh
Discharge through orifice in time interval
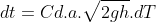
As the volume of liquid leaving the tank is equal to the volume of liquid flowing through orifice in time dT, we have
A (- dh) = Cd . a . √2gh . dT
-ve sign is inserted because with the increase of time, head on orifice decrease.
 or
or
By integrating the above equation between
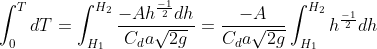
![T=\frac{-A}{C_{d}.a.\sqrt{2g}}\left [ \frac{h^{\frac{-1}{2}+1}}{\frac{-1}{2}+1} \right ]_{H_{1}}^{H_{2}}~=\frac{-A}{C_{d}.a.\sqrt{2g}}\left [ \frac{\sqrt{h}}{\frac{1}{2}} \right ]_{H_{1}}^{H_{2}}](https://latex.codecogs.com/gif.latex?T=\frac{-A}{C_{d}.a.\sqrt{2g}}\left&space;[&space;\frac{h^{\frac{-1}{2}+1}}{\frac{-1}{2}+1}&space;\right&space;]_{H_{1}}^{H_{2}}~=\frac{-A}{C_{d}.a.\sqrt{2g}}\left&space;[&space;\frac{\sqrt{h}}{\frac{1}{2}}&space;\right&space;]_{H_{1}}^{H_{2}})
For emptying the tank completely ,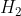 = 0 and hence
= 0 and hence
--------------------------------------------------------------------------------------------------------------------------
a = Area of the orifice
H1 = Initial height of the liquid
H2 = Final height of the liquid
T = Time in seconds for the liquid to fall from H1 to H2 .
Let at any time, the height of liquid from orifice is h and let the liquid surface fall by a small height dh in time dT.
Then,
Volume of liquid leaving the tank in time,dT = A × dh
Also,
The theoretical velocity through orifice,
Discharge through orifice/sec
dQ = Cd × Area of orifice × Theoretical velocity
= Cd.a.√2gh
Discharge through orifice in time interval
As the volume of liquid leaving the tank is equal to the volume of liquid flowing through orifice in time dT, we have
A (- dh) = Cd . a . √2gh . dT
-ve sign is inserted because with the increase of time, head on orifice decrease.
By integrating the above equation between
For emptying the tank completely ,





Comments
Post a Comment